name of picture

Ehsan Elhamifar

EECS Department
University of California, Berkeley

Email:
ehsan [at] eecs [dot] berkeley [dot] edu

Address:
University of California, Berkeley
TRUST Center
Room 337 Cory Hall
Engineering Department
Berkeley, Ca 94720-1774

Phone:
510-643-5105

Ehsan Elhamifar

Postdoctoral Fellow
Electrical Engineering and Computer Science Department
University of California, Berkeley

Sparse Subspace Clustering

    Project Summary
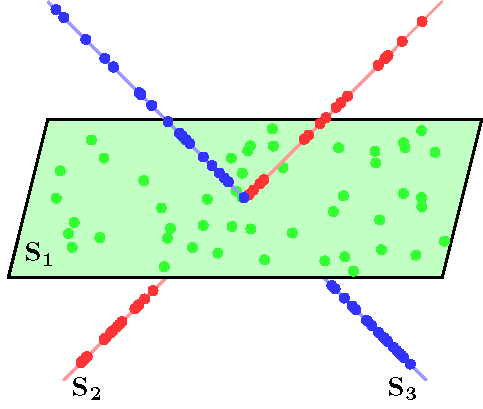
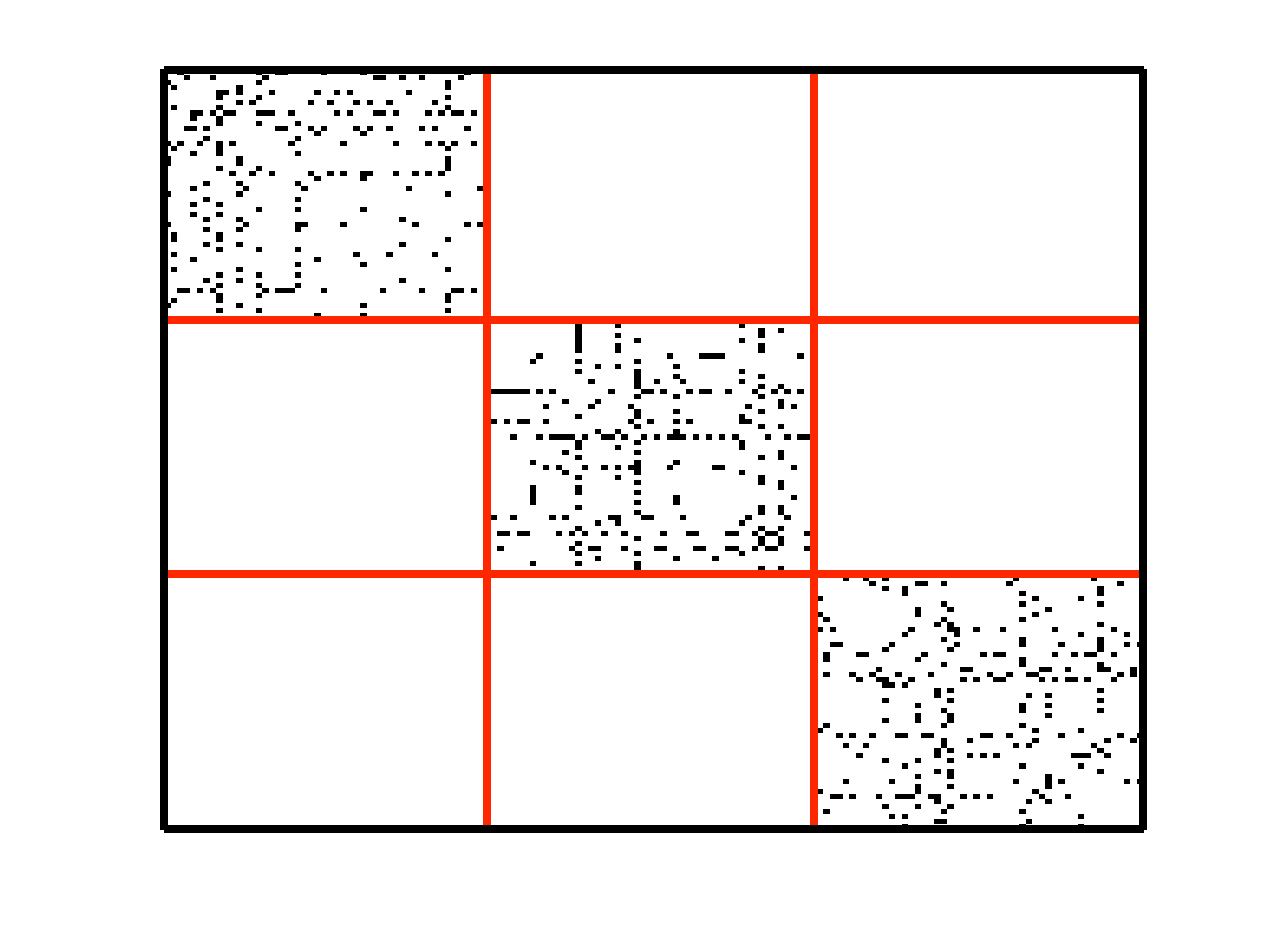
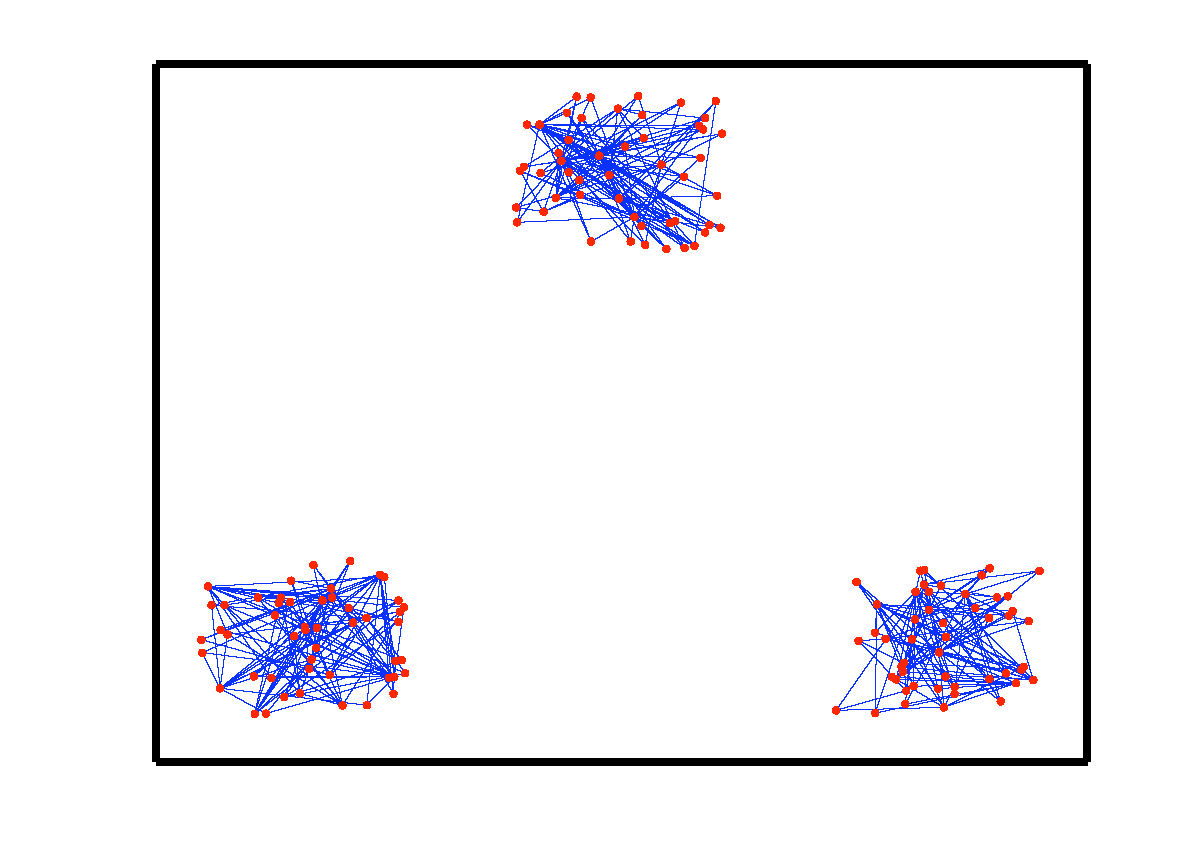
    Subspace clustering is an important problem with numerous applications in image processing and computer vision. Given a set of points drawn from a union of linear or affine subspaces, the task is to find segmentation of the data. In most applications the data are embedded in high-dimensional spaces, while the underlying subspaces are low-dimensional. In this project, we propose a new approach to subspace clustering based on sparse representation. We exploit the fact that each data point in a union of subspaces can always be written as a linear or affine combination of all other points. By searching for the sparsest combination, we automatically obtain a representation from points lying in the same subspace. This allows us to build a similarity matrix, from which the segmentation of the data can be easily obtained using spectral clustering. While in principle finding the sparsest representation is an NP hard problem, we show that under mild assumptions on the distribution of the data across subspaces, the sparsest representation can be found efficiently by solving a convex optimization problem.

    SSC Algorithm
    Let { S1, ..., Sn } be an arrangement of n linear subspaces of dimensions { d1, ..., dn } embedded in D dimensional space. Consider a given collection of N = &sum i Ni data points { y1, ..., yN } drawn from the n subspaces. The sparse subspace clustering (SSC) algorithm [1], addresses the subspace clustering problem using techniques from sparse representation theory. This algorithm is based on the observation that each data point y &isin Si can always be written as a linear combination of all the other data points in { S1, ..., Sn }. However, generically, the sparsest representation is obtained when the point y is written as a linear combination of points in its own subspace. In [1] we show that when the subspaces are low-dimensional and independent (dimension of the sum is equal to the sum of dimensions), this sparse representation can be obtained by using L1 minimization. The segmentation of the data is found by applying spectral clustering to a similarity graph formed using the sparse coefficients. More specifically, the SSC algorithm proceeds as follows.


    An example of data drawn from three subspaces and the corresponding adjacency matrix and similarity graph is shown in the figure below. For each data point, the L1 minimization picks points from the same subspace, hence the adjacency matrix has a block-diagonal structure and the similarity graph has three connected components. Thus, using standard spectral clustering methods, we can recover the components of the similarity graph, hence the segmentation of the data.

    Data drwan from 3 subspaces Matrix of sparse coefficients Similarity graph

    However, requiring the subspaces to be independent is a strong assumption in practice. In [2], we address the more general problem of clustering disjoint subspaces (each pair of subspaces intersect only at the origin). We show that under certain conditions relating the principal angles between the subspaces and the distribution of the data points across all the subspaces, the sparse coefficients can still be found by using convex L1 optimization. This result represents a significant generalization with respect to the sparse recovery literature, which addresses the sparse recovery of signals in a single subspace. The subspace clustering problem is also much more challenging than block-sparse recovery problem, whose goal is to write a signal as a linear combination of a small number of known subspace bases. First, we do not know the basis for any of the subspaces nor do we know which data points belong to which subspace. Second, we do not have any restriction on the number of subspaces, while existing methods require this number to be large.

    Extensions of SSC
    The SSC method shown in the Algorithm 1, is based on the assumption that the data are perfect (without noise) and lie on multiple linear subspaces. The algorithm can be modified to take into account noise in the data. When data points are contaminated with noise, we propose to solve the stable L1 minimization problem for each data point yi:
    where &lambda is a trade-off parameter between sparsity of the solution and the reconstruction error. A smaller value for &lambda favors sparsity while a larger value for &lambda results in a more dense coefficient vector but lower reconstruction error. The SSC method can also deal with affine subspaces, missing data, as well as outlying entries. Please refer to [1] for detailed information.

    Application to Motion Segmentation
    We apply SSC to the motion segmentation problem, i.e., the problem of separating a video sequence into multiple spatiotemporal regions corresponding to different rigid-body motions in the scene. This problem is often solved by extracting a set of points in an image, and tracking these points through the video. Under the affine projection model, all the trajectories associated with a single rigid motion live in a low-dimensional subspace. Therefore, the motion segmentation problem reduces to clustering a collection of point trajectories according to multiple subspaces. We evaluate SSC on the Hopkins155 motion database, which is available online at http://www.vision.jhu.edu/data.htm. The database consists of 155 sequences of two and three motions which can be divided into three main categories: checkerboard, traffic, and articulated sequences. The following table shows the results of SSC as well as the state of the art on the Hopkins 155 database (feature trajectories are projected into 4n dimensional space with n being the number of motions). The SSC algorithm achieves an average misclassification rate of 1.24% on the whole database, which is a significant improvement over the state of the art. Please see [1] for detailed information about the experiments.


    Misclassification rates on the Hopkins 155 database

    Algorithm GPCA LLMC LSA RANSAC MSL SCC ALC SSC
    Average 10.34% 5.93% 4.94% 9.76% 5.03% 2.33% 3.56% 1.24%
    Median 2.54% 0.63% 0.90% 3.21% 0.00% - 0.50% 0.00%


    Code
    Please visit the Code Page for the Matlab implementation of SSC.


    Publications

    [1] E. Elhamifar and R. Vidal, Sparse Subspace Clustering,
    IEEE International Conference on Computer Vision and Pattern Recognition, 2009.

    [2] E. Elhamifar and R. Vidal, Clustering Disjoint Subspaces via Sparse Representation,
    IEEE International Conference on Acoustics, Speech, and Signal Processing, 2010.

    [3] E. Elhamifar and R. Vidal, Sparse Subspace Clustering: Algorithm, Theory, and Applications,
    IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI), 2013.

    [4] M. Soltanolkotabi, E. Elhamifar, and E. J. Cand�s, Robust Subspace Clustering,
    Annals of Statistics, 2014.

Back to home