Boundary Layer Separation
Flow separation is a phenomenon of widespread interest in boundary layer theory and its understanding was advanced considerably by Stewartson and Williams (1969) who showed that regular separation could occur by an interactive process; see also Neiland (1969) and Messiter (1970). Since then, triple deck theory has contributed much to the understanding of boundary layer separation.
Excellent reviews may be found in Stewartson (1981), Messiter (1983) and Smith (1986). Finally, Sychev et al. (1997) is the translation of the first textbook (Sychev, 1990) on this fascinating subject. Two book chapters have been written by Rothmayer and Smith (1998). More recently, an introductory book on interactive boundary layer theory has been written by Ian Sobey (2000).
Thermal boundary layer separation
There are many examples of fluid flows in technology and engineering where imposed boundary conditions or geometries results in flow separation. In applications where thermal effects are significant, such as cooling or insulating systems, such separations can have important consequences for the heat transfer properties of the system.
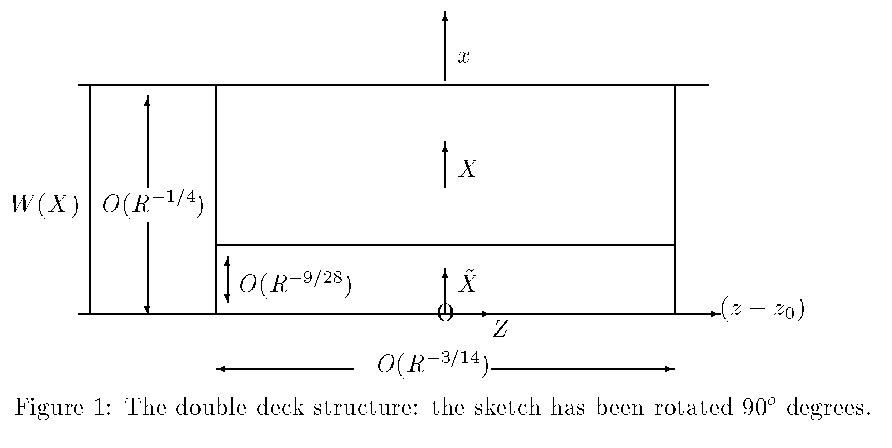
Currently we are considering the manner in which a thermal jet flow, such as that driven by buoyancy along a heated vertical wall, can separate resulting in a drastic reduction in heat transfer through the wall. Such separations may be relevant, for example, where the jet encounters a corner, obstruction or sudden change in thermal boundary conditions.
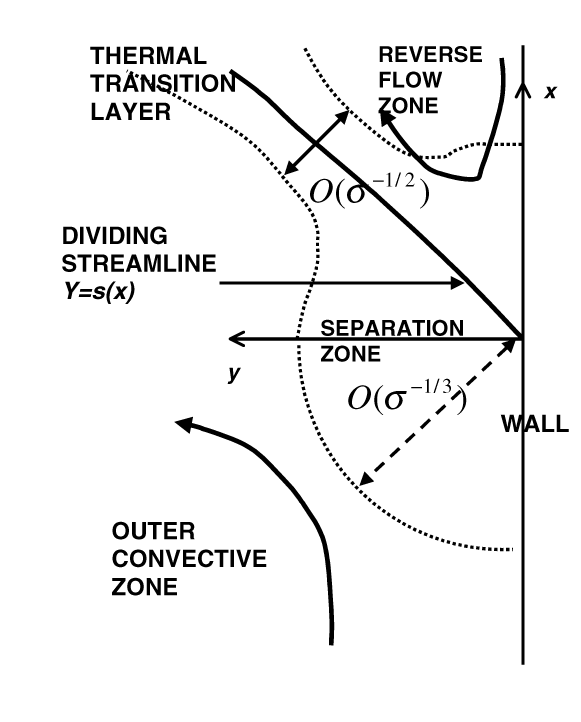
One important aspect of such flows is the role of the Prandtl number. Present work aims to investigate the flow development at high Prandtl numbers where inertial effects are suppressed at the expense of buoyancy, leading to the possibility of the thermal field playing a significant role in the local separation process. Results have been presented for the separation zone at finite Prandtl numbers, where locally the flow is controlled by viscosity and inertia, independent of thermal effects. Nevertheless the resulting temperature field is of some interest and its calculation is a natural first step in the analysis of high Prandtl number separating flows.
- Stewartson, K. and Williams, P.G. (1969) Self induced separation. Proc. Roy. Soc. London, A312, pp 181-206.
- Stewartson, K. (1981) D'Alembert's paradox. SIAM Rev., 23, pp 308-43.
- Messiter, A.F. (1970) Boundary layer flow near the trailing edge of a flat plate. SIAM J. Appl. Math. 18: 241-257.
- Neiland, V. Ya. (1969) Towards a theory of separation of the laminar boundary layer in a supersonic stream." Mekh. Zhid. Gaza, 4, pp 53-57 (English translation in Fluid Dynamics, 4, pp 33-35)
- Messiter, A.F. (1983) Boundary layer interaction theory. Trans. ASME J. Appl. Mech., 50, pp 1104-13.
- Rothmayer, A.P. and Smith, F.T. (1998) Free-Interactions and Breakaway Separation and Numerical Solution of Two-Dimensional Steady Triple-Deck Problems in The Handbook of Fluid Dynamics
- Smith, F.T. (1986) Steady and unsteady boundary layer separation. Ann. Rev. Fluid Mech., 18, pp 197-220.
- Sychev, V.V. (1990) Asymptotic theory of boundary layer separation. Nauka, Moscow, Russia.
- Sychev, V.V., Ruban, A.I., Sychev, V.V. and Korelev, G.L. (1998) Asymptotic theory of separated flows. Cambridge University Press.
- Sobey, I.J. (2000)Introduction to Interactive Boundary Layer Theory. Oxford University Press. See also http://www.sjc.ox.ac.uk/scr/sobey/iblt
Papers
- Reversed flow calculation of high Prandtl number thermal boundary layer separation. JT Ratnanather and PG Daniels. 4th International Symposium on Transport Phenomena in Heat and Mass Transfer, University of New South Wales, Sydney, Australia. July 14-19, 1991.
- Solution of the thermal
boundary layer equations in regions of flow reversal.
JT Ratnanather and PG Daniels. SIAM Journal of Applied Mathematics, Vol 55, No 1, pp 192-204, 1995.
Note (added Aug 12, 2001): Streamwise steplength restriction for Box method was shown by RS Fisk "On an oscillation phenomenon in the numerical solution of the diffusion-convection equation". SIAM J. Numer. Anal. 19(4),721-724. - On the thermal field of a separating wall jet. PG Daniels and JT Ratnanather. Journal of Engineering Mathematics, Vol 41, No 4, pp 329-344. 2001.
A computational challenge
The last three papers demonstrate why the free interaction of a separating thermal boundary layer is a formidable computational problem. In a nutshell, a forward-backward parabolic partial differential equation over an unbounded domain needs to be solved. The following strategy could confirm the asymptotic results reported in Daniels & Ratnanather (2001):- Keller Box (or Crank Nicholson) solution strategy for forward-backward parabolic equation described in Ratnanather & Daniels (1995) and Daniels & Ratnanather (2001); could instead consider a Saintlos, Mauss & Rigal (1994) numerical scheme
- Use the Page & Riley (1985) implementation of Downstream-Upstream InTeractive (DUIT) scheme of Williams (1975) with downstream boundary conditions from Smith & Duck (1977), Ratnanather & Daniels (1991) and Daniels & Ratnanather (2001)
- First solve the Smith-Duck (1977) free
interaction problem and then the thermal free interaction.
- Daniels, P.G. & Ratnanather, J. T. (2001) On the thermal field of a separating wall jet. Journal of Engineering Mathematics. 41, 329-344.
- Page, M.A. & Riley, N. (1985) The free interaction of a supersonic-flow over a porous wall. Q. J. Mech. App. Math. 38,79-92.
- Ratnanather, J.T. & Daniels, P.G. (1995) Solution of the Thermal Boundary Layer Equations in Regions of Flow Reversal. SIAM J. App. Math, 55, 192-204.
- Saintlos, S., Mauss, J. & Rigal, A. (1994) Local relaxation method for boundary-layer equations with separation. Int. J. Engng. Science 32, 409-416.
- Smith, F. T. & Duck, P. W. (1977) Separation of jets or thermal boundary-layers from a wall. Q. J. Mech. App. Math. 30, 143-156.
- Williams, P.G. (1975) A reverse-flow computation in the theory of self-induced separation. (Proc. 4th Int. Conf. Numerical Methods in Fluid Dynamics) Lecture Notes in Physics, 35, 445-451.
