Quadrant Tree Classifier
Document
Information
Package base
version 2.8.0
1/5/2009
Project 5: Statistical
Learning with Multi-Scale Cardiovascular Data
Contact email: [email protected]
Index
1.1. Sensitivity and Specificity
1.3.1. Empirical Distribution Function
1.3.2. Kaplan-Meier Estimator, Censoring and Truncation
The quadrant tree
classifier is based on the idea of selecting a pair of numerical or ordered
features x, y, choosing thresholds c, d for each feature breaking up the
feature space into four quadrants based on which inequalities x<c, x>c
and y<d, y>d hold. Such a
classifier amounts to a tree (stub) of depth two in which the same
classification criterion for splitting is used for the two nodes at depth two. Constraining the available trees in this
manner reduces the level of complexity of the space of allowable classifiers
and can thus help to avoid over-fitting while providing a search space that is
computationally simpler to exhaustively search.
In addition, our
aim is to produce a classifier having a high degree of sensitivity with optimum
specificity, so build these criteria into the search through the classifier
space, identifying what is an optimum pair of features in the sense of
maximizing apparent specificity subject to the constraint that the apparent
sensitivity is above a prescribed level.
The search for
feature pairs and corresponding thresholds requires calculations involving
likelihoods as well as survival probabilities. We will break the discussion of these two aspects of the
problem and introduce them one by one in the following sections.
1.1. Sensitivity and Specificity
The most
important concepts in quadrant tree classifier are sensitivity and
specificity. They are statistical
measures of the performance of a classification test. The sensitivity measures the proportion of actual positives
which are correctly identified as such (or, in our case, the percentage of
"fired" patients who are identified as "fired"); and the specificity
measures the proportion of negatives which are correctly identified (i.e. the
percentage of "not-fired" patients who are identified as
"not-fired"). They are
closely related to the concepts of type I and type II errors.
Consider, as an
example, a scenario we have been investigating, in which heart disease patients
implanted with cardioverter-defibrillators. Firing of the device is used by us as a surrogate phenotype
for sudden cardiac death. When
this occurs, we say that the device has "fired". We are trying to build a model to
identify these subjects who will "fire". The model outcomes for patients are "fired" or
"not-fired". Since the model
is not 100% accurate, the actual "fired" (or "not-fired")
status of each person may be different. In that setting:
* True "fired":
Patients whose devices fail are correctly identified as "fired"
* False "fired":
Patients whose devices do not fail are wrongly identified as "fired"
* True "not-fired":
Patients whose devices do not fail are correctly identified as "not-fired"
* False "not-fired":
Patients whose devices fail are wrongly identified as "not-fired"
Then,
Sensitivity =
number of true "fired" / (number of true "fired" + number
of false "not-fired")
i.e. patients who
are correctly diagnosed as "fired" / "fired" patients in
total
Specificity =
number of true "not-fired" / (number of true "not-fired" +
number of false "fired")
i.e. patients who
are correctly diagnosed as "not-fired" / "not-fired" patients
in total
We can put them
in a table.
|
|
"fired" patients |
"not-fired" patients |
|
Identified as "fired" |
A = True "fired" |
B = False "fired" (Type I error,) |
|
Identified as "not-fired" |
C = False "not-fired" (Type II error) |
D = True "not-fired" |
|
|
Sensitivity = A / (A + C) |
Specificity = B / (B + D) |
Conditional
probability plays an important role in our quadrant tree classifier. Conditional probability is the
probability of some event A, given the occurrence of some other event B,
denoted as 
.
Conditional
probability can be calculated as:
The numerator 
is called joint
probability. That is, it is the
probability of both events occurring.
It is also written as 
.
Based on
conditional probability, we can solve more complicated problems in our
setting. For example, A is
an event that can be caused by events 
. If we are given
that event A occurred, what is probability of 
occurring, i.e. 
? We can use conditional probability to solve this problem.
Where 
Each term in the
formula has a conventional name:
* 
is the
conditional probability of 
, given A.
It is also called the posterior probability because it is derived from
or depends upon the specified value of A.
* 
is the prior
probability or marginal probability of 
. It is
"prior" in the sense that it does not take into account any
information about A.
* 
is the prior or
marginal probability of A.
The last piece of
quadrant tree classifier is survival analysis. It is a part of statistics which specifically models death
time and failure time, or more generally, the time to event data. In our case, fire or failure is
considered an "event". In
our case, survival analysis attempts to answer questions such as: what is the probability
of patients not firing until a certain time? How do particular circumstances or
individual characteristics increase or decrease the probability of firing?
The primary
interest in survival analysis is survival function, conventionally denoted S,
which is defined as
where t is
a time, T is a random variable denoting the time of death. So the survival function is the
probability that the time of fire (or failure) is later than some specified
time.
There are many
ways to estimate S(t). We
will briefly discuss about them in the following sections:
1.3.1. Empirical Distribution
Function
The first and
simplest method is just using only those in study for at least some time t
and taking the ratio between it and the total number of observations. (i.e. empirical
distribution function)
This method is
simplest, but not be the best. Subjects
who have only been observed for s time units are removed from
consideration if s<t . Thus
we may be leaving out useful information. On the other hand, this method does lead to an unbiased
estimate of the probability of firing before t time units since implant.
1.3.2. Kaplan-Meier Estimator,
Censoring and Truncation
To solve the
problem that empirical distribution function has, that is, being unbiased when
patients are not observed for sufficient amount of time, we introduce another
method --- Kaplan-Meier estimator (product limit estimator). It is developed to address the censored
and truncated data, which is what we mostly deal with in the analysis.
Censoring (or
right censoring) happens when patients are not observed for a sufficient amount
of time, then we do not know whether and when they get "fired" or
not. All we know is that they do not get "fired" when they are in the
study. This is the most common
type of censoring in our analysis since a lot of patients participate in the
study only for a very short time, then decide to leave or lose contact with the
hospital. Even so, their cases are
still informative to us, thus we want to use their cases to give us more
information about the firing. In
order to put their cases in use, we only take them into consideration during
the period when they are in the study.
This is the basic idea of Kaplan-Meier estimator. And this is also how Kaplan-Meier is
better than empirical distribution function.
Kaplan-Meier
estimator apparently uses more information than empirical distribution
function, which makes it more efficient.
Kaplan-Meier estimator takes these patients who leave the study into
consideration. For example, to
estimate a survival probability at a particular time t, empirical
distribution function only counts these who survive pass time t. And all
the calculation is based on this group of patients. It ignores patients who drop off in the middle of the study
(before time t). These
patients may also survive pass time t, but they are assumed to have "fired"
at the minute when they leave the study, which is an unreasonable
assumption. On the other hand, to
estimate the same probability, Kaplan-Meier estimator starts from the beginning
time of the study and calculate the conditional survival probability at every
possible times before t, and multiple them together to get a more
accurate estimate, or in some sense, less biased estimate than empirical
distribution function.
Kaplan-Meier
estimator can be unbiased when under the assumption that censoring times are
independent with "fired" times.
When these two types of times are independent, then censoring do not
give us any information about when these patients who get censored are going to
get "fired". So we can
treat censoring times as random times.
But if they are dependent with each other, then censoring may mean
something to us. For example, say
patients tend to drop off the study when they feel bad and uncomfortable with
their cardioverter-defibrillators, then there is a tendency that patients get "fired"
soon after they drop off the study, or vice versa. If that is the case, then every conditional probability in
the Kaplan-Meier estimator is biased, thus the Kaplan-Meier estimator is
biased. In our analysis, there is
no guarantee that this assumption is true, so we cannot say Kaplan-Meier estimator
is unbiased either. But it at
least uses all the information we have about firing, so Kaplan-Meier estimator
is usually preferred over empirical distribution function.
Besides
censoring, truncation (or left-truncation) is also a major problem in our analysis.
It happens when some patients join the study a while after they are implanted
with cardioverter-defibrillators, so we do not observe them before they join
in, which means everything we observe from them are based on the fact that they
join the study after time t. This gives us the problem that everything
we get is conditional. This
problem can also be solved by Kaplan-Meier estimator since it only takes
patients into consideration when they are in the study. And everything in Kaplan-Meier estimator
is conditional (conditional survival probability). So truncation can be easily solved by Kaplan-Meier
estimator. But again, Kaplan-Meier
estimator is only unbiased when truncation times are independent with "fired"
times. The reason is similar to that
of censoring which is mentioned in the previous paragraph. For example, if patients tend to go
back to the hospital when they sense that their cardioverter-defibrillators are
malfunctioning, then there is also a tendency that patients get fired soon after
they join in the study. So
Kaplan-Meier estimator is biased in that case.
In general,
Kaplan-Meier estimator is a milestone for survival analysis. It is a very
simple idea and yet improves the estimation quality by significant magnitude. The paper of Kaplan-Meier estimator is
also one of the top 5 most referenced papers in this field.
To conduct Kaplan-Meier
estimator, we first list all unique death times 
, and get number at risk 
and number of death
at each
time. Number of risk 
is the number of
patients who are alive and in the study just before 
. Number of
death 
is the number of
patients who died at time 
. Then the Kaplan-Meier
estimator is:
If there is no
censored or truncated data, then 
. So Kaplan-Meier
estimator becomes 
. We can see
that it is just the empirical estimate function.
Other than the
methods mentioned above, there are still a great number of methods. For example, Proportional hazard rate
model is also an important model.
It is developed under the assumption that each individual's hazard rate
function is proportional to the others' over the time.
Under the
proportional hazard rate assumption, we can assume there is a baseline hazard
rate and everyone else's hazard rate functions are just proportional to the
baseline. So we can just estimate
the effect parameter(s) without any consideration of the hazard function. This approach is also called Cox
proportional hazard rate model. Cox
model is a semiparametric method since we only put the effect parameters in the
model but the baseline has no parameters at all.
With the introduction
to all these fundamental knowledge, let's move to the quadrant tree classifier.
Quadrant tree
classifier is developed based on traditional tree model, with only two features
and two thresholds. These
thresholds break up the feature space into four quadrants based on which
inequalities x<tx, x>ty, y<ty and y>ty holds, at mean time, the
thresholds also break the dataset into four pieces which will be used for
estimating survival probabilities.
See the graph below.
|
|
x >
tx |
|
|
y >
ty |
x<tx, y>ty |
x>tx,
y>ty |
|
x<tx, y<ty |
x>tx, y<ty |
|
Within each
quadrant i (i=1,2,3,4), we conduct a survival analysis based on the dataset of
that quadrant. So we can estimate
the probability of fire before/after a certain point (a threshold we
pre-specified), i.e. P(fired before threshold | quadrant i) and P(fired
after threshold | quadrant i), or simply P(fired | quadrant i) and P(not-fired
| quadrant i).
Since we divide
the original dataset into four parts.
We can estimate the probability of any individual falls into each of the
quadrant by:
Now we have P(fired
| quadrant i) (from survival analysis) and P(quadrant i), we can apply
the conditional probability to get P(quadrant i | fired) and P(quadrant
i | not-fired), denoted as Pi and Qi respectively.
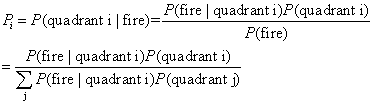
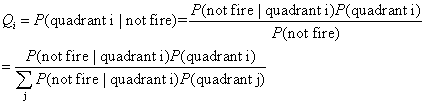
Now we have eight
probabilities Pi and Qi i=1,2,3,4. We calculate the likelihood ratio (=Pi/Qi) for every
quadrant i, and put them in descending order. For example, we have a set of Pi and Qi like
this:
|
Quadrant |
Pi |
Qi |
Likelihood
ratio |
|
1 |
0.5 |
0.25 |
0.2 |
|
2 |
0.2 |
0.1 |
2 |
|
3 |
0.35 |
0.35 |
1 |
|
4 |
0.4 |
0.3 |
1.33 |
After put them in
descending order based on likelihood ratio, they become the following table:
|
Quadrant |
Pi |
Qi |
Likelihood ratio |
Indicator for specificity |
(1-indicator for specificity)*Qi |
|
2 |
0.2 |
0.1 |
2 |
1 |
0 |
|
4 |
0.4 |
0.3 |
1.33 |
1 |
0 |
|
3 |
0.35 |
0.35 |
1 |
0.86 = (0.9-0.6
)/0.35 |
0.05=
(1-0.86)*0.35 |
|
1 |
0.05 |
0.25 |
0.2 |
0 |
0.25 =
(1-0)*0.25 |
|
Sum (rows 1-2) |
0.6 |
|
|
|
|
|
Sum (rows 1-4) |
1 |
1 |
|
|
0.3
(specificity) |
Starting with the
quadrant which has the largest likelihood ratio, we take summation of their Pi's
by including them in one by one based on the likelihood ratio order. We stop doing that when the summation
reaches the largest number below the sensitivity (including sensitivity). In our case, we set our sensitivity to
be 90%, so after we include quadrant 2 and 4, we stop, otherwise, the summation
will go over 0.9.
Then we assign 1s
to each quadrant whose Pi's are included in the summation, call it
"indicator for specificity".
For the quadrant who just missed to be included, we calculate the
difference between the sensitivity and summation, divide it by Pi of
that quadrant, and assign the ratio to the indicator. In our case, the summation is 0.6, the sensitivity is 0.9,
the quadrant's Pi is 0.35. So, for
quadrant 3, the indicator is 0.86 = (0.9 - 0.6 )/ 0.35. For the rest of quadrants, assign 0s
for the indicator. In our case, it
is quadrant 1.
The indicators
mean that: if it is 1, then persons falling in this quadrant will be identified
as "fired". If it is 0,
then persons falling in this quadrant will be identified as "not-fired". If it is a fraction p, then persons
falling in this quadrant will be randomly identified as "fired" with
a probability p, and identified as "not-fired" with a probability
1-p.
After this
setting, we can lock the sensitivity at 90%. It is because sensitivity is the probability of being
identified as "fired" given "fired" patients, i.e. P(identified
as "fired" I "fired" patients). So, in our case, it is can be written as:
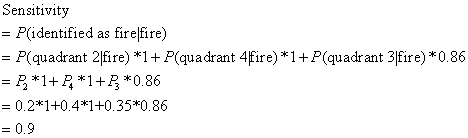
With the fixed
sensitivity, we can get the maximized specificity. Since specificity is the probability of being identified as "not-fired"
given "not-fired" patients, i.e. P(identified as "not-fired"
I "not-fired" patients).
So it is can be written as:
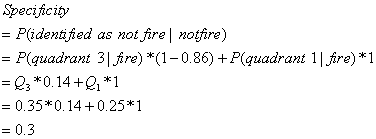
Now, with a
threshold and a sensitivity given, we can repeat the procedure above with
different criterions (tx and ty) and find an optimal pair of tx and ty with the
largest specificity. This is
basically how the quadrant tree classifier work.
2.1. Commented Code (download here)
library(survival)
#
# Given vector of
event times and fired indicator (0=censored,1=fired),
# and a time
threshold, compute an estimate of the probability of firing
# before that
time threshold. We use linear interpolation of output from the
# survival package's
kaplan-meier calculation. Generally, we err on the side
# of making the
probability greater than needed to be careful.
#
survival.prob<-function(time,fired,time.threshold)
{
# If no data, then returen 0 so
err on the side of making everyone fire.
if (length(time)==0)
{
return(0)
}
# Fit a survival model with
Kaplan-Meier method.
S<-survfit(Surv(time,fired),type="kaplan-meier")
# Assign number of observatoins
to ntimes.
ntimes<-length(S$time)
# If there is just one observation
or the smallest time is larger than the
# threshold, return 0.
if
((ntimes==1)||(min(S$time)>=time.threshold))
{
return(0)
}
# If the largest time is smaller
than the threshold, return the largest survival
# probability generated by the
model.
if
(max(S$time)<=time.threshold)
{
return(S$surv[length(S$surv)])
}
# If not either of the two
situation mentioned above, then do linear interpolation
# Find the index of observation
with the largest time that is smaller than threshold
index1<-max(which(S$time<time.threshold))
# Find the index of observation
with the smallest time that is larger than threshold
# i.e. index1+1
index2<-index1+1
# Calculate the probability of
surviving after time index1.
p1<-S$surv[index1]
# Calculate the probability of
surviving after time index2.
p2<-S$surv[index2]
# Linear interpolation
lambda<-(time.threshold-S$time[index1])/(S$time[index2]-S$time[index1])
p<-p1+lambda*(p2-p1)
return(p)
}
build.quadrant.classifier<-function(x,y,implanted,days.to.firing,tx.list,ty.list,sens,time.threshold)
{
#
#
#
# Inputs:
#
# x =
continuous feature variable vector
# y =
continuous feature variable vector
# implanted
= days of implanted
# days
to firing = days to firing
#
# tx =
list of x thresholds
# ty =
list of y thresholds
# sens =
desired sensitivity
#
time.threshold = time defining the "fired within" phenotype
#
#Output:
#
# an
assignment of probabilities to the cells:
#
# cell
1: x<tx, y<ty
# cell
2: x<tx, y>ty
# cell
3: x>tx, y<ty
# cell
4: x>tx, y>ty
#
#
# This function uses the R
"survival" package to compute
# Kaplan-Meier probabilities
#
# Create a time variable and an
indicator of fired.
#
# Assign lx the value of the
length of x.
lx<-length(x)
# Assign fired a array of 0s with
length the same as lx.
fired<-rep(0,lx)
# Assign time a array of 0s with
length the same as lx.
time<-rep(0,lx)
# Remove all the NAs and convert
data for survival analysis.
for (i in seq(1,lx))
{
# For each i,
i.e. each observation:
# If
days.to.firing is NA, then assign both fired[i] and time[i] to 0.
# Otherwise, if
days.to firing is smaller than time.threshold, then assign
# fired[i]
if
(is.na(days.to.firing[i]))
{
fired[i]<-0
time[i]<-implanted[i]
} else
# Otherwise, if
days.to firing is smaller than time.threshold, then assign
# fired[i] 1,
and copy days.to.firing[i] to time[i]. And otherwise, assign
# fired[i] 0,
and copy implanted[i] to time[i].
{
if (days.to.firing[i]<time.threshold)
{
fired[i]<-1
time[i]<-days.to.firing[i]
}else
{
fired[i]<-0
time[i]<-implanted[i]
}
}
}
#
# Get rid of missing data
#
# Combine x, y, time, and fired
to a data frame named d.temp
d.temp<-data.frame(x=x,y=y,time=time,fired=fired)
# Remove all the observations
with missing data or NAs.
d.temp<-d.temp[complete.cases(d.temp),]
#
# Creat a list with spec=0
best.L<-list(spec=0)
# Creat a loop to try every
possible combination of tx and ty to get a optimal
# pair of tx ty with maxium
specificity.
for (tx in tx.list)
{
for (ty in
ty.list)
{
#
#
Break up the data into the four cells based on tx and ty.
#
data<-list()
data[[1]]<-d.temp[(d.temp$x<tx)&(d.temp$y<ty),]
data[[2]]<-d.temp[(d.temp$x<tx)&(d.temp$y>ty),]
data[[3]]<-d.temp[(d.temp$x>tx)&(d.temp$y<ty),]
data[[4]]<-d.temp[(d.temp$x>tx)&(d.temp$y>ty),]
#
#
#
Compute prior probabilities of the cells.
#
p.cells<-c(
dim(data[[1]])[1],
dim(data[[2]])[1],
dim(data[[3]])[1],
dim(data[[4]])[1])
p.cells<-p.cells/sum(p.cells)
#
#
Compute the fire survival probablilities.
#
Note the linear interpolation.
#
#
Creat array for p and P[fire | cell = i]
p.fire<-c()
#
Creat array for p and P[not fire | cell = i]
p.notfire<-c()
#
#
Do a loop for each cell.
for
(i in seq(1,4))
{
#print("i = ")
#print(i)
# Store time for cell i
time<-data[[i]]$time
# Store fired for cell i
fired<-data[[i]]$fired
# Do survival analysis within cell i
p<-survival.prob(time,fired,time.threshold)
#print("p = ")
#print(p)
# Store P[not fire | cell = i] to p.notfire
p.notfire<-c(p.notfire,p)
# Store P[fire | cell = i] to p.fire
p.fire<-c(p.fire,1-p)
}
#print("end of loop p.fire p.notfire= ")
#print(p.fire)
#print(p.notfire)
#
#
We estimated P[fire | cell = i] for each i,
#
and P[not fire | cell = i]
#
for each i and we know P[ cell = i].
#
Use Bayes theorem to get the cell
# distributions under each
class.
#
# p
= P[ cell = i | fired]
#
#
and
#
# q
= P[ cell i | not fired]
#
#
Calculate P[ cell = i, fired]
p<-p.fire*p.cells
# Calculate P[ cell = i |
fired]
p<-p/sum(p)
#
Calculate P[ cell = i, not fired]
q<-p.notfire*p.cells
#
Calculate P[ cell = i | not fired]
q<-q/sum(q)
#
#
Compute likelihood ratios
#
lr<-p/q
#
#
Make a list of the cell indices 1,2,3,4 in decreasing order
#
of likelihood ratio.
#
perm<-order(lr, decreasing=TRUE)
#
#
Define the cell probabilities for the classifier.
#
The rule is to assign a
#
probability of 1 to each cell until we get to
#
the desired sensitivity.
#
The last probability can be a fraction in order
#
to get exactly what we want.
#
#print("lr = ")
#print(lr)
#print("p = ")
#print(p)
#print("q = ")
#print(q)
#
#
Assign all 0s to fprob
fprob<-rep(0,4)
#
Creat a variable used in "while" loop.
psum<-0
i<-1
#
Repeat the loop until psum+p[perm[i]]<sens, which means keep add up more
#
cells into psum until it reaches sensitiviy.
while(psum+p[perm[i]]<sens)
{
# If a
cell is included, assign fprob for that cell 1.
fprob[perm[i]]<-1
# Add
one more into psum
psum<-psum+p[perm[i]]
i<-i+1
}
#
For the last cell, compute a partial
fprob[perm[i]]<-(sens-psum)/p[perm[i]]
#
#
Compute the specificity
#
spec<-sum((1-fprob)*q)
#
If we find a larger specificity, we replace the best.L with the new one.
if
(spec>best.L$spec)
{
best.L<-list(fprob=fprob,spec=spec,tx=tx,ty=ty,p=p,q=q)
}
}
}
# Return best.L.
best.L
}
2.2. Uncommented Code (download here)
library(survival)
survival.prob<-function(time,fired,time.threshold)
{
# If no data, then returen 0 so
err on the side of making everyone fire.
if (length(time)==0)
{
return(0)
}
S<-survfit(Surv(time,fired),type="kaplan-meier")
ntimes<-length(S$time)
if
((ntimes==1)||(min(S$time)>=time.threshold))
{
return(0)
}
if
(max(S$time)<=time.threshold)
{
return(S$surv[length(S$surv)])
}
index1<-max(which(S$time<time.threshold))
index2<-index1+1
p1<-S$surv[index1]
p2<-S$surv[index2]
lambda<-(time.threshold-S$time[index1])/(S$time[index2]-S$time[index1])
p<-p1+lambda*(p2-p1)
return(p)
}
build.quadrant.classifier<-function(x,y,implanted,days.to.firing,tx.list,ty.list,sens,time.threshold)
{
lx<-length(x)
fired<-rep(0,lx)
time<-rep(0,lx)
for (i in seq(1,lx))
{
if
(is.na(days.to.firing[i]))
{
fired[i]<-0
time[i]<-implanted[i]
} else
{
if (days.to.firing[i]<time.threshold)
{
fired[i]<-1
time[i]<-days.to.firing[i]
}else
{
fired[i]<-0
time[i]<-implanted[i]
}
}
}
d.temp<-data.frame(x=x,y=y,time=time,fired=fired)
d.temp<-d.temp[complete.cases(d.temp),]
best.L<-list(spec=0)
for (tx in tx.list)
{
for (ty in
ty.list)
{
data<-list()
data[[1]]<-d.temp[(d.temp$x<tx)&(d.temp$y<ty),]
data[[2]]<-d.temp[(d.temp$x<tx)&(d.temp$y>ty),]
data[[3]]<-d.temp[(d.temp$x>tx)&(d.temp$y<ty),]
data[[4]]<-d.temp[(d.temp$x>tx)&(d.temp$y>ty),]
p.cells<-c(
dim(data[[1]])[1],
dim(data[[2]])[1],
dim(data[[3]])[1],
dim(data[[4]])[1])
p.cells<-p.cells/sum(p.cells)
p.fire<-c()
p.notfire<-c()
for
(i in seq(1,4))
{
time<-data[[i]]$time
fired<-data[[i]]$fired
p<-survival.prob(time,fired,time.threshold)
p.notfire<-c(p.notfire,p)
p.fire<-c(p.fire,1-p)
}
p<-p.fire*p.cells
p<-p/sum(p)
q<-p.notfire*p.cells
q<-q/sum(q)
lr<-p/q
perm<-order(lr, decreasing=TRUE)
fprob<-rep(0,4)
psum<-0
i<-1
while(psum+p[perm[i]]<sens)
{
# If a
cell is included, assign fprob for that cell 1.
fprob[perm[i]]<-1
# Add
one more into psum
psum<-psum+p[perm[i]]
i<-i+1
}
fprob[perm[i]]<-(sens-psum)/p[perm[i]]
spec<-sum((1-fprob)*q)
if
(spec>best.L$spec)
{
best.L<-list(fprob=fprob,spec=spec,tx=tx,ty=ty,p=p,q=q)
}
}
}
best.L
}