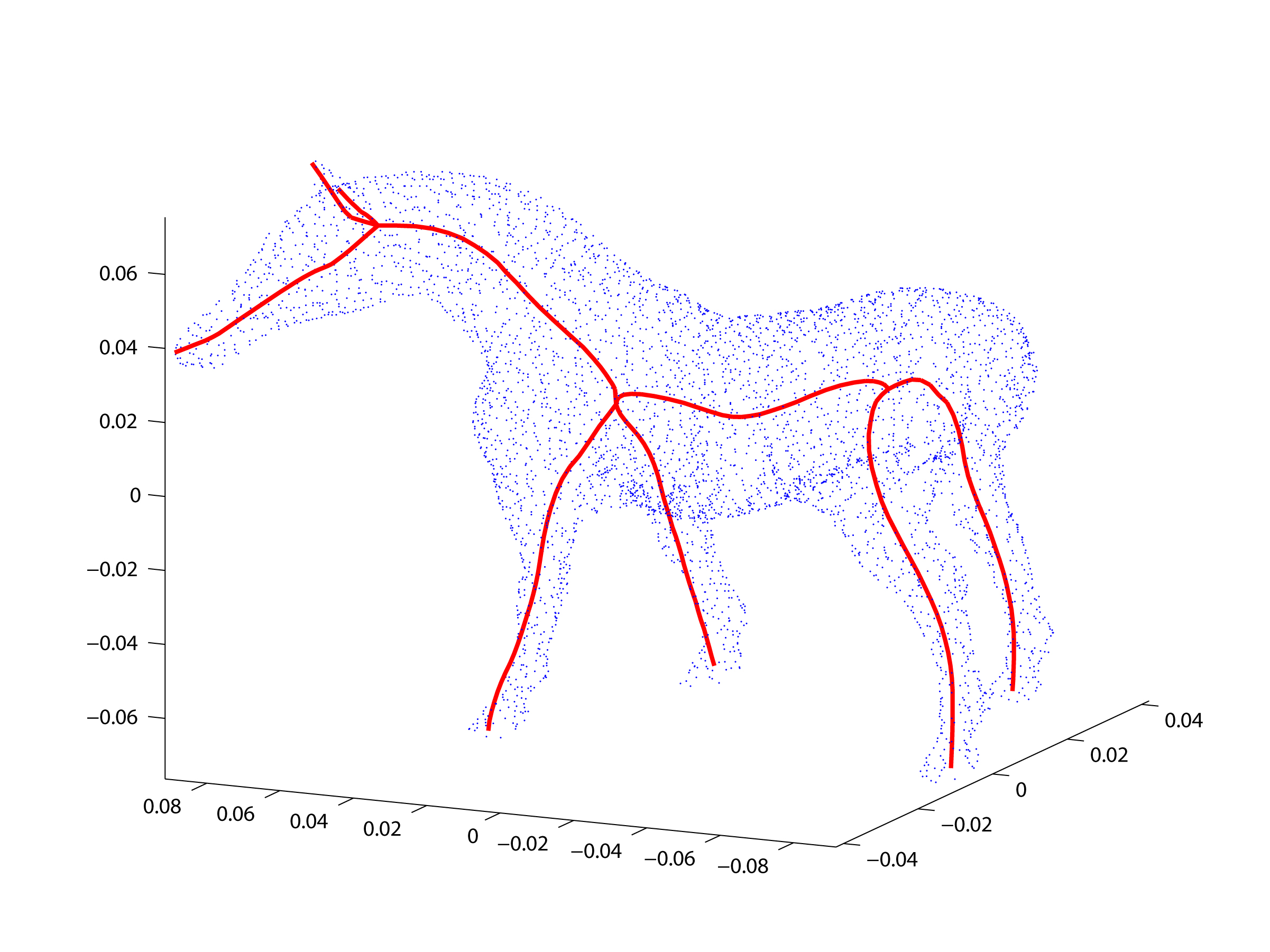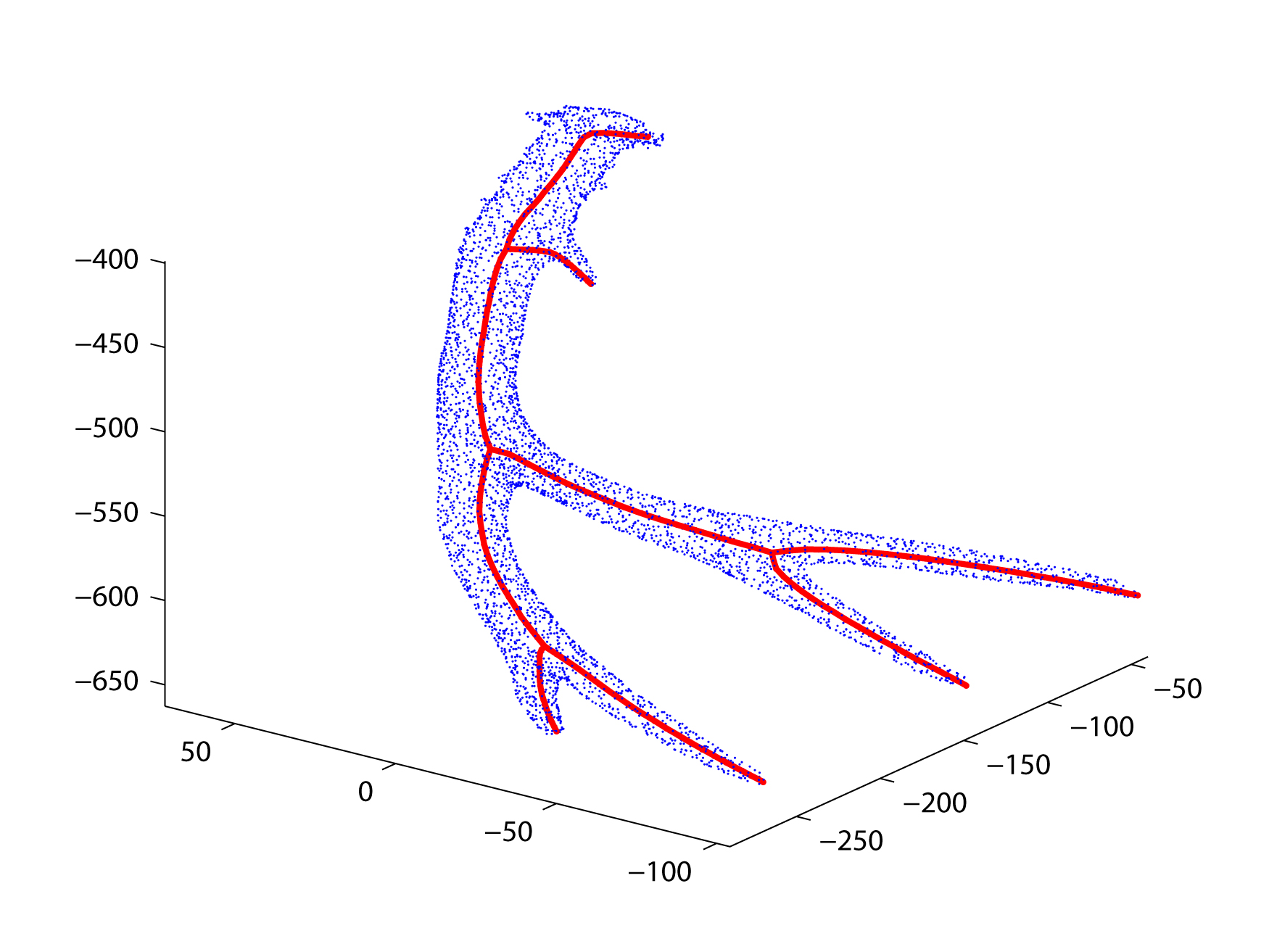
Axis of Generalized Cylinder
Generalized cylinders model uses hierarchies of cylinder-like modeling
primitives to describe shapes. It captures many of our intuitions about axes of
symmetry and hierarchical description. The axes of symmetry form the skeleton of
the shape. A generalized cylinder is a surface created by moving a cross section
along an axis. The axis is a space curve and the cross section can be
transformed by rotation, scaling, or distortion during the motion. We would like
to give a natural and intuitive definition of axis for cylindrical shapes. For
2D shapes, the medial axis is a good candidate, though it is sensitive to
perturbations. For 3D shapes, the medial scaffold is often complicated surfaces
and does not match people's intuitions very well. We give a new definition of
axis for generalized cylinders based on principal curves. This approach uses a
regression point of view, defining the axis as a minimization point of a energy
function. We prove the existence of a solution and give the equations of the
minimization point. We also apply the definition to some real and artificial
examples and get good results. Our goal is to produce natural and intuitive
shape descriptions for 2D and 3D shapes. We believe that is essential for
building general objects recognition systems. It would be also useful in shape
analysis, classification and compression.