Since shapes outlines are often represented with two-dimensional curves, many shape-space models arise from the design of spaces of plane curves. Such spaces are generally associated to smoothness (differentiability) requirements for the curves, and come with a metric space structure since comparing shapes has important practical applications. Most of the spaces of plane curves that have been proposed in the literature actually possess richer structures, many of them providing infinite-dimensional Riemannian manifolds. In such spaces, the distance is associated to paths of least energy in shape space, yielding optimal shape evolutions, or geodesics. It is important to remark that shape spaces are not exactly spaces of curves, but are built upon them via identification of equivalent classes. For example, curves that are deduced for each other by translation, rotation and scaling correspond to the same shape and can be considered as equal. This results in spaces of shapes represented as quotients spaces of curves via the action of some linear transformations. Finally, one should define shapes regardless of their parametrization, which induces a new quotient, this time by the group of diffeomorphism of the unit interval, or of the unit circle for closed curves.

The following papers all discuss a special shape space on which geodesics are relatively easy to compute, because the associated space of curves turns out to be isometric to a Hilbert space. In references [1 - 4], it is noticed that quotienting for  scale results in identifying the shape space to Hilbert sphere. This argument is pushed further in reference [5], in which it is noticed that quotienting for rotation with closed curves results in an identification of the shape space with a Grassmann manifold. 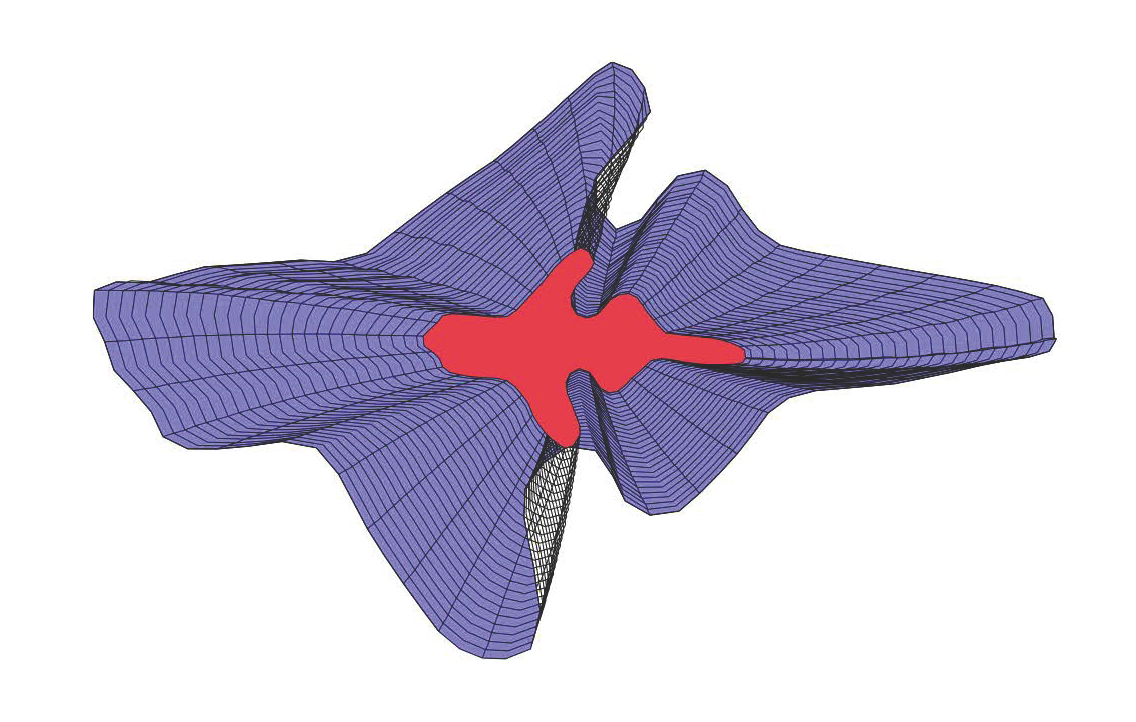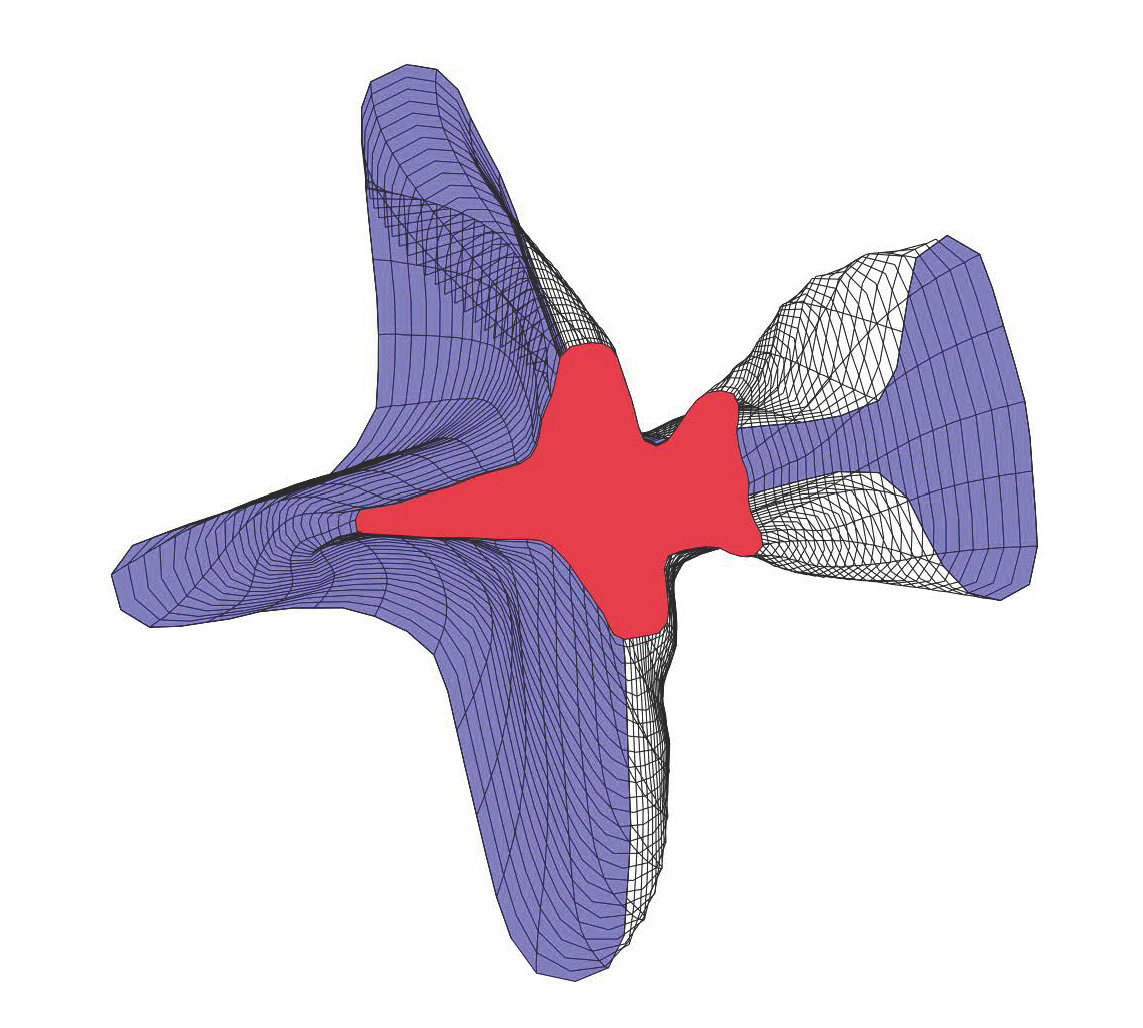The images below illustrate some geodesic paths in curve space between selected shapes.

Reference [6] generalizes these results to arbitrary dimensions and large parameter classes, while presenting them in a different angle (that of metamorphosis ).

[1] A distance for elastic matching in object recognition (Summary) L. Younes, Comptes rendus de l'Académie des sciences. Série 1, Mathématique  322  197--202  (1996)
[2] A distance for elastic matching in object recognition, R. Azencott and F. Coldefy and L. Younes, Pattern Recognition, 1996., Proceedings of the 13th International Conference on  1  687--691  (1996)
[3] Computable elastic distances between shapes, L. Younes, SIAM Journal on Applied Mathematics  58  565--586  (1998)
[4] Optimal matching between shapes via elastic deformations, L. Younes, Image and Vision Computing  17  381--389  (1999)
[5] A metric on shape space with explicit geodesics, L. Younes, PW. Michor, D. Mumford and J. Shah, Rend. Lincei Mat. Appl. 19 (2008) 25-57.
[6] Elastic distance between curves under the metamorphosis viewpoint arXiv:1804.10155, published in Chapter 12.7 of Shapes and Diffeomorphisms.

The next two papers discuss a class of curve matching problems that include the one introduced in reference 1-4 above, and study their properties, regarding, in particular, the existence of minimizers.
[7] Diffeomorphic matching problems in one dimension: Designing and minimizing matching functionals, A. Trouvé and L. Younes, Computer Vision-ECCV 2000    573--587  (2000)
[8] On a class of diffeomorphic matching problems in one dimension, A. Trouvé and L. Younes, SIAM Journal on Control and Optimization  39  1112--1135  (2000)

Note that many of these results and compiled and extended in Elastic Metrics on Spaces of Euclidean Curves: Theory and Algorithms by Bauer et al.